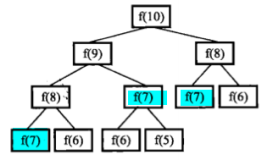
我们都知道斐波那契数（也叫兔子数）是一组十分有趣的数字，首相为1，第二项也是1，之后的每一项就是前两项之和，那么该如何实现输入第n项就打印其对应的斐波那契数字呢？

递归实现
事实上，要实现斐波那契数的打印并不困难，最简单的思路就是递归。

递归就是将斐波那契数计算过程进行提炼，进而得出一段递归。

代码如下：

include<stdio.h>

int fabonacci(int n)
{

if (n == 1 || n == 2)
    return 1;//第一项和第二项直接返回1
else
    return fabonacci(n - 1) + fabonacci(n - 2);

}
int main()
{

int n = 0;
while (~scanf("%d",&n))
{
    printf("%d\n", fabonacci(n));
}
return 0;

复制代码
要想得出递归的思路最重要的就是掌握递归的核心：大事化小！

可是,递归就可以完全解决斐波那契数吗？

事实上，当我们输入50，既要打印第50项的数字时，递归的代码就会要运算很长的时间，这是因为递归不会记住之前的项的结果，所以求的项数越大，就会进行越多的重复计算，就会严重拖慢结果的打印时间。

那么我们该如何进行代码的优化呢？

循环实现
这个时候就可以使用循环来会解决递归重复进行计算的问题了

我们可以将第一项和第二项定义为a和b，c=a+b，然后依次进行推移，就可以实现打印斐波那契数了

include<stdio.h>

int fabonacci(int n)
{

int a = 1;
int b = 1;
int c = 0;
if (n == 1 || n == 2)
    return 1;
while (n-2)//减2是因为要在第三次才会进行移位
{
    c = a + b;
    a = b;
    b = c;
    n--;
}
return c;

}
int main()
{

int n = 0;
while (~scanf("%d",&n))
{
    printf("%d\n", fabonacci(n));
}
return 0;

}

复制代码
使用循环实现斐波那契数的效率就会大大增加

变式
Fibonacci数列是这样定义的： F[0] = 0 F[1] = 1 for each i ≥ 2: F[i] = F[i-1] + F[i-2] 因此，Fibonacci数列就形如：0, 1, 1, 2, 3, 5, 8, 13, ...，在Fibonacci数列中的数我们称为Fibonacci数。给你一个 N，你想让其变为一个Fibonacci数，每一步你可以把当前数字X变为X-1或者X+1，现在给你一个数N求最少需要多少步可以变为Fibonacci数。

这里是斐波那契数数列，第一个数字是0，第二个数字是1，与上面的稍微有一点不一样，但是不影响思路

在这里我们只需要关心如何判断输入的数字n与斐波那契数的两个间距的最小间距。

要是n与b相等则说明n就是斐波那契数，所以最小偏移量就是0。

要是n介于两个斐波那契数之间，就要取距离n最近的间距。

include<stdio.h>

include<math.h>

int main()
{

int a = 0;
int b = 1;
int c = 0;
int n = 0;
while (~scanf("%d", &n))
{
    while (1)
    {
        if (n == b)
        {
            printf("0\n");
            break;//记得跳出循环
        }
        if (n>a&&n<b)
        {
            if (abs(n - a) < abs(b - n))
            {
                printf("%d\n", abs(n - a));
                break;
            }
            else
            {
                printf("%d\n", abs(b - n));
                break;
            }
        }
        c = a + b;
        a = b;
        b = c;
    }
}
return 0;

}