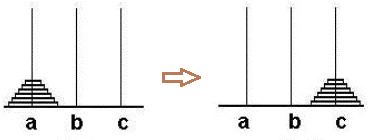
汉诺塔背景
在印度有这样一个古老的传说,相传大梵天在创造世界的时候,做了三根金刚石柱,在其中一根柱子上从上而下叠着64片黄金圆盘,于是大梵天就要求婆罗门按圆盘的大小重新摆在另外一根柱子上
要求:一次只能移动一根柱子,并且在移动的过程中,也要保持大盘在小盘的下面
image-20220423122213504
汉诺塔思路
首先,假设只有一个盘子,那么直接从A到C即可
当有两个盘子的时候就将上面的较小的盘子先挪到B,再将较大的盘子挪到C上,最后将B
上的较小的盘子放到C上即可
那么,当有3个及以上盘子的时候,就应该有一种整体递归的思维,递归的核心就是大事化小,总结出重复的步骤,找出规律
由于要保证最后大盘子要在小盘子的下面,所以可以将所有盘子看做两个部分,分为最下面最大的盘子和上面剩下的盘子这两部分,可以先将剩下的盘子这个整体从A经过C的中转,再放到B上面。接着再处理最大的盘子,直接放到C,最后再处理剩下的盘子这个整体,可以将他们从B先放到A上中转,再放到C即可
/**
- hanoi中参数解释:
- pos1是指盘子的起始位置
- pos2是指盘子的中转位置
- pos3是指盘子的终点位置
*/
public static void move(char pos1, char pos2) { //进行打印移动的过程
System.out.print(pos1 + "->" + pos2 + " ");
}
public static void hanoi(int n, char pos1, char pos2, char pos3) {
if (n == 1) {
move(pos1, pos2);//当盘子为1的时候直接从A移到C
} else {
hanoi(n - 1, pos1, pos3, pos2);
move(pos1, pos3);
hanoi(n - 1, pos2, pos1, pos3);
}
}
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
while (scanner.hasNext()) {
int n = scanner.nextInt();
hanoi(n, 'A', 'B', 'C');
System.out.println();
}
}复制代码
以上就是关于汉诺塔问题的求解,主要就要理解其中的递归实现 最后,欢迎大家点赞收藏关注,感谢大家的支持!