机器学习：从公式推导到代码实现一元线性回归

什么是线性回归

我们有一个数据集D={(X1,Y1),(X2,Y2),(X3,Y3).....)}，把这组数据可视化出来如图所示：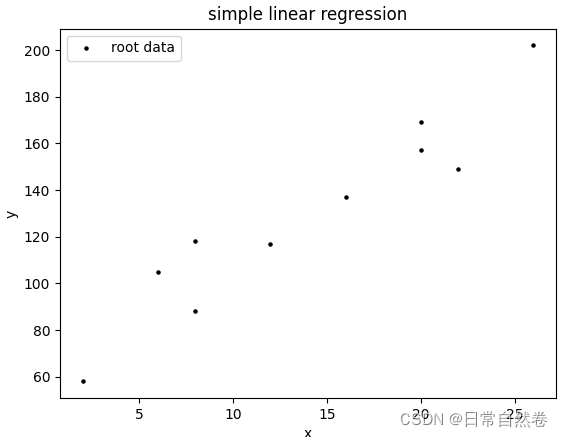

线性回归通俗易懂的说就是通过这些点中找到一条直线使这条直线到每个点的距离最小，我们在寻找这条直线的过程就叫做线性回归。图中点的横坐标也叫自变量，如果自变量的维度是1，那么就叫做一元线性回归（如（1,2，3）），相反，如果不是1如（（1,2），（1,3）），那么就叫做多元线性回归。
最终结果如下：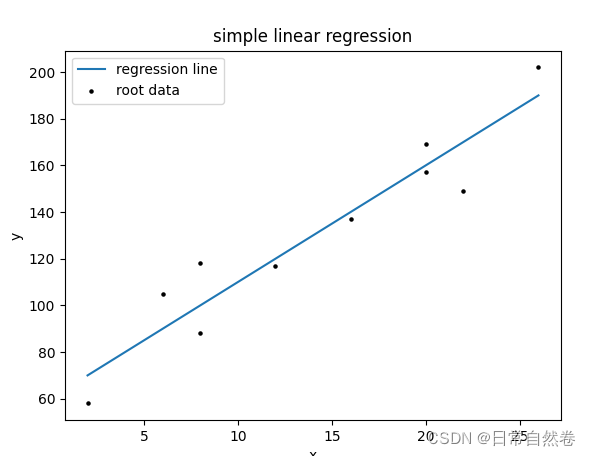

求解过程

我们如果想找到这条直线，首先设一个方程：Yi=w*Xi+b,我们通过数据集已知x和y，只要我们在知道w和b，那么我们就求解完成。我们要找的这条直线是距离每个点最近的，我们采用最小二乘估计来求解，这个方法的思路就是算出所有点到直线的距离（每个点到直线的距离我们采用均方误差的方式计算），我们会得到一个带有未知数的函数，如图所示：

E(w,b)为LossFunction，是关于w与b的凸函数（判断函数的凹凸性可通过函数的二阶导数判断），形状类似于y=x^2的U形曲线,所有函数的极值点就是它的最小值点，我们对E（w，b）分别求偏导数，这样就可以得出w，b的最优解。求解过程如图所示：
对w求解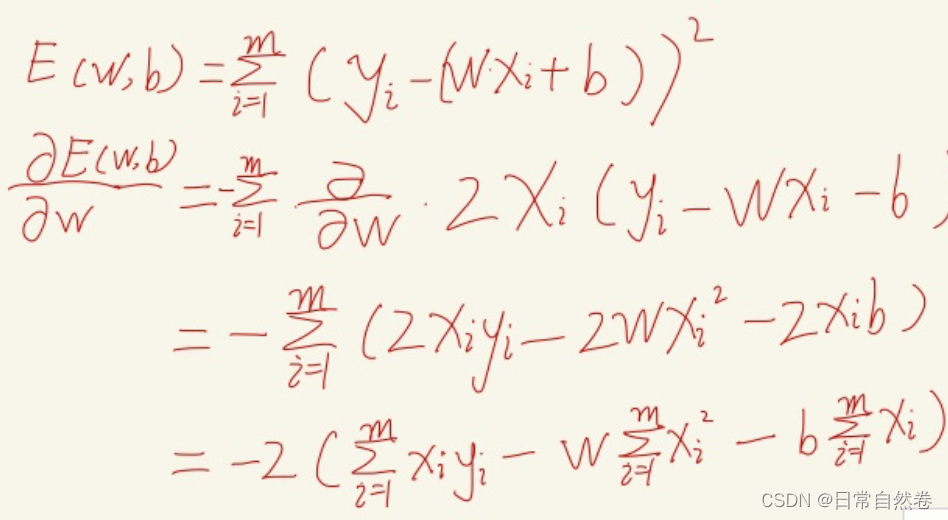

对b求解偏导数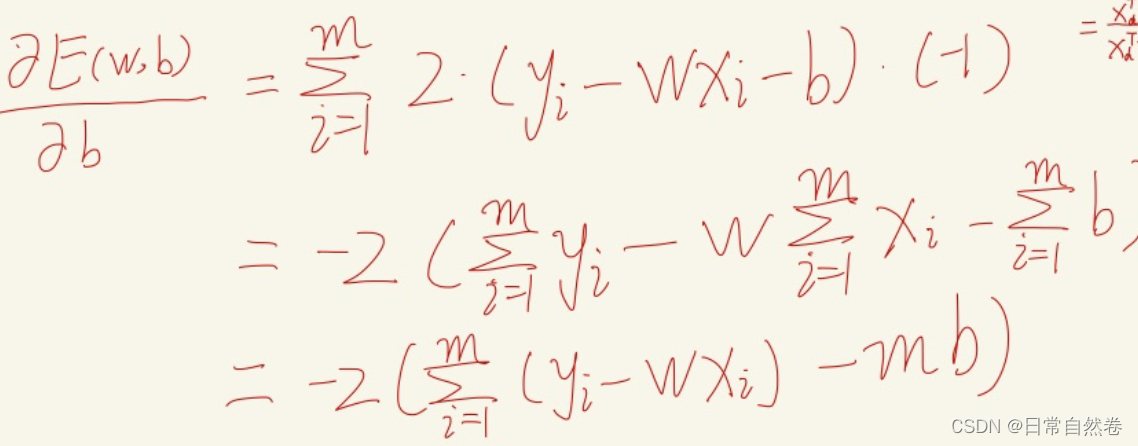

使b的偏导数=0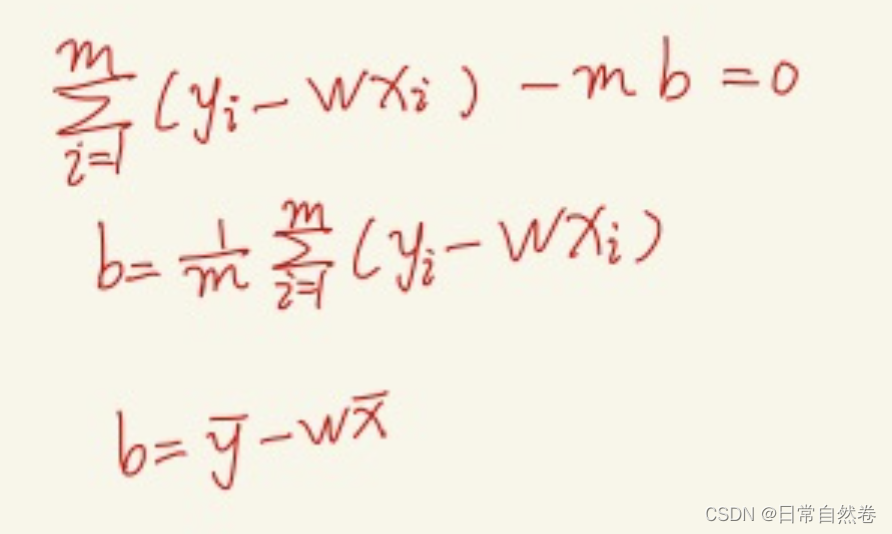

我们把这个式子带入上面的对w求偏导数=0的式子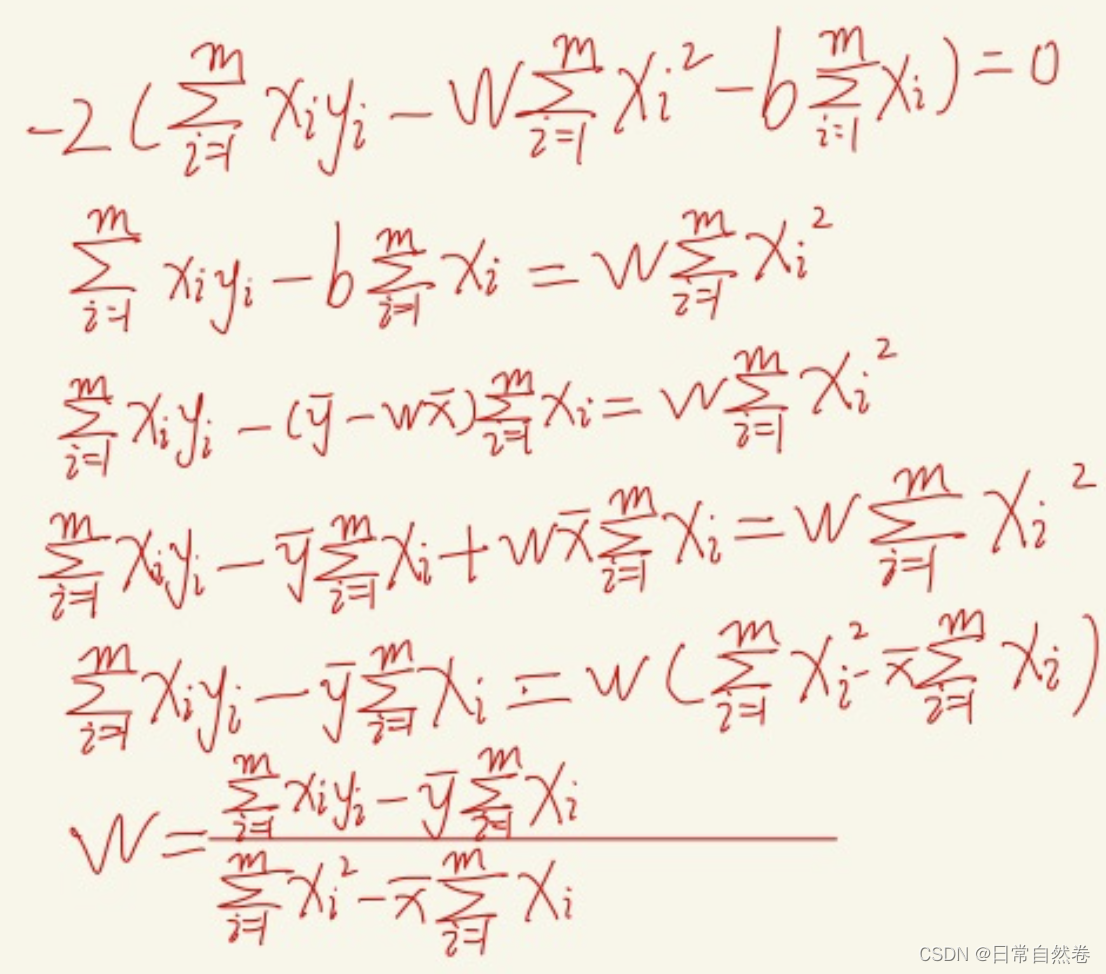


化简得到：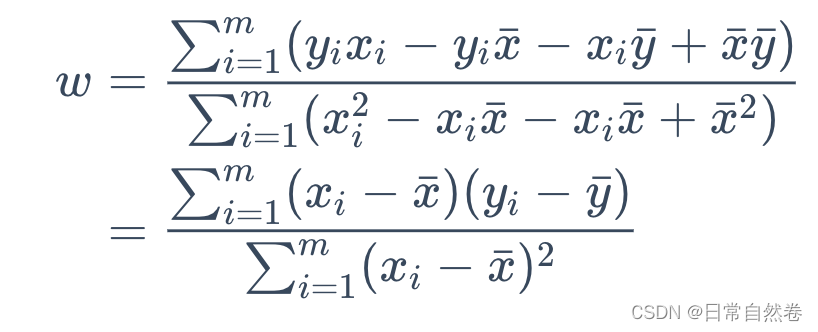

通过w求出b
上述代码我们可以通过python的for循环方式实现，如果我们想通过numpy库的矩阵加速方式实现，我们需要的关于w的公式继续化简
化简方式：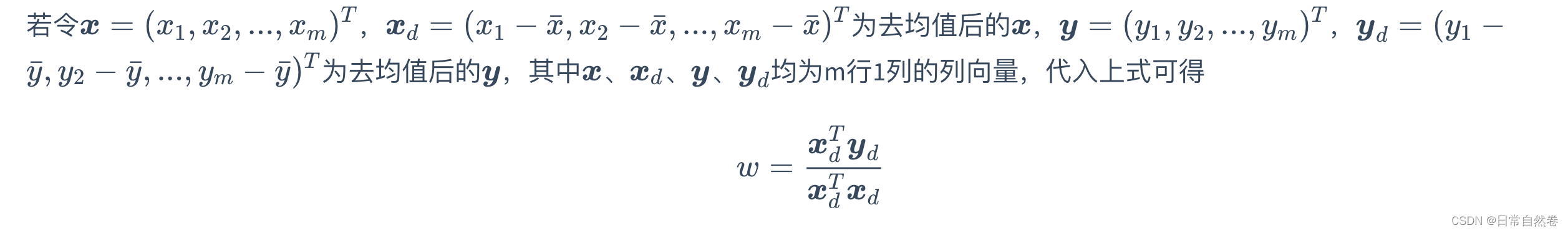

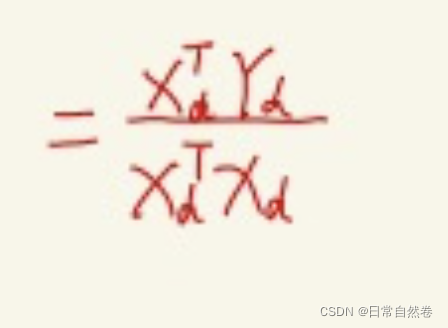
代码实现

import numpy as np

import matplotlib.pyplot as plt


class One_model(object):
    def __init__(self, x, y):
        self.x = x
        self.y = y
        self.x_mean = np.mean(self.x)
        self.y_mean = np.mean(self.y)

#传统算法计算
    def train_tradition(self):
        parameter = []
        for i in range(len(self.x)):
            w1 = ((self.x[i] - self.x_mean) * (self.y[i] - self.y_mean))
            w2 = (self.x[i] - self.x_mean) * (self.x[i] - self.x_mean)
            parameter.append([int(w1), int(w2)])
        w1 = int(0)
        w2 = int(0)
        for i in parameter:
            w1 += i[0]
            w2 += i[1]
        w = w1 / w2
        b = self.y_mean - w * self.x_mean
        print('tradition parameter', 'w:', w, 'b:', b)
        return w, b

    def train_matrix(self): #矩阵加速运算
        w1 = np.dot((self.x - self.x_mean), (self.y - self.y_mean))
        w2 = np.dot((self.x - self.x_mean), (self.x - self.x_mean))
        w = w1 / w2
        b = self.y_mean - w * self.x_mean
        print('matrix parameter', 'w:', w, 'b:', b)

    def data_view(self):  # 绘制回归线
        # 绘制
        plt.scatter(self.x, self.y, label='root data', color='k', s=5)  # s 点的大小
        plt.plot(self.x, 5 * self.x + 60, label='regression line')
        plt.xlabel('x')
        plt.ylabel('y')
        plt.legend()
        plt.title('simple linear regression')
        plt.show()
        return


if __name__ == '__main__':
    x = np.array(list([2, 6, 8, 8, 12, 16, 20, 20, 22, 26]))
    y = np.array(list([58, 105, 88, 118, 117, 137, 157, 169, 149, 202]))
    demo1 = One_model(x, y)
    demo1.train_tradition()
    demo1.data_view()

    # x1=int(input(111))
    # One_model.predict(x1)