一、今日知识点总结
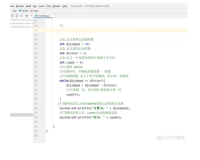
一、循环语法重拾:
for(循环初始化表达式; 循环条件表达式; 循环执行表达式) { 循环体 }
二、运作过程的重新认识
以前曾经傻傻的认为for循环是先执行括号里中三个表达式,然后再执行循环体部分的内容。emmmm,太呆萌了…
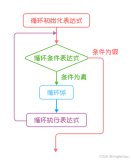
对于常用的for循环,它的运作过程为:
1、执行 循环初始化表达式
2、执行循环条件表达式。如果表达式的值为真,则执行循环体,否则结束放弃循环
3、执行完循环体之后,再执行循环执行表达式。也就是对循环变量进行更新。
4、重复上面的步骤2和步骤3,知道控制循环结束与否的循环表达式判断出来,结果为假,那么结束循环。
三、碎碎念
感觉循环是真的挺重要的,但是我很容易忽视它,就像我现在正在准备的暴力杯一样,很多前辈都说会for就好
二、今日做题记录
第一题:剑指 Offer 64. 求1+2+…+n
题目描述
剑指 Offer 64. 求1+2+…+n 求 1+2+...+n ,要求不能使用乘除法、for、while、if、else、switch、case等关键字及条件判断语句(A?B:C)。 示例 1: 输入: n = 3 输出: 6 示例 2: 输入: n = 9 输出: 45 限制: 1 <= n <= 10000
解题报告
题目中说的是不然使用循环和乘法,学数据结构的树这一章的时候,很多小伙伴应该都写过把递归改非递归的习题,那么,我们现在把非递归的循环改为递归。
递归唯一需要注意的是设置递归的边界,对于这个题而言,递归的边界就是进行递归累加的数,是否为0
参考代码(C++)
class Solution { public: int sumNums(int n) { n && (n += sumNums(n-1)); return n; } };
第二题:231. 2 的幂
题目描述
231. 2 的幂 给你一个整数 n,请你判断该整数是否是 2 的幂次方。如果是,返回 true ;否则,返回 false 。 如果存在一个整数 x 使得 n == 2x ,则认为 n 是 2 的幂次方。 示例 1: 输入:n = 1 输出:true 解释:20 = 1 示例 2: 输入:n = 16 输出:true 解释:24 = 16 示例 3: 输入:n = 3 输出:false 示例 4: 输入:n = 4 输出:true 示例 5: 输入:n = 5 输出:false 提示: -231 <= n <= 231 - 1 进阶:你能够不使用循环/递归解决此问题吗?
解题报告
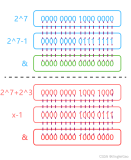
这个题倒是常规的可爱枚举了,只是需要注意的是要使用unsigned来处理整数溢出的情况
参考代码(C++版本)
class Solution { public: bool isPowerOfTwo(int n) { //处理特殊情况 if(n <= 0) return false; if(n == 1) return true;//2的零次方 //用无符号类型处理溢出情况 unsigned int ans = 1; //常规的枚举,注意整数的边界是2的31-1 for(int i = 1; i <= 31;i++) { ans *= 2; if(ans == n) return true; } return false; } };
第三题:326. 3 的幂
题目描述
326. 3 的幂 给定一个整数,写一个函数来判断它是否是 3 的幂次方。如果是,返回 true ;否则,返回 false 。 整数 n 是 3 的幂次方需满足:存在整数 x 使得 n == 3x 示例 1: 输入:n = 27 输出:true 示例 2: 输入:n = 0 输出:false 示例 3: 输入:n = 9 输出:true 示例 4: 输入:n = 45 输出:false 提示: -231 <= n <= 231 - 1 进阶:你能不使用循环或者递归来完成本题吗?
解题报告
这个题和上面的例题就没有什么大的区别了,只是要换成3去不断的乘,同时注意边界,算了一下,应该只能枚举到20;
参考代码(C++版本)
class Solution { public: bool isPowerOfThree(int n) { //处理特殊情况 if(n <= 0) return false; if(n == 1) return true;//3的零次方 //用无符号类型处理溢出情况 unsigned int ans = 1; //常规的枚举,注意3的21次方大概就超了 for(int i = 1; i <= 20;i++) { ans *= 3; if(ans == n) return true; } return false; } };
第四题:342. 4的幂
题目描述
342. 4的幂 给定一个整数,写一个函数来判断它是否是 4 的幂次方。如果是,返回 true ;否则,返回 false 。 整数 n 是 4 的幂次方需满足:存在整数 x 使得 n == 4x 示例 1: 输入:n = 16 输出:true 示例 2: 输入:n = 5 输出:false 示例 3: 输入:n = 1 输出:true 提示: -231 <= n <= 231 - 1
解题报告
一样的,换汤不换药,注意边界,此时只能到15啦
参考代码(C++版本)
class Solution { public: bool isPowerOfFour(int n) { //处理特殊情况 if(n <= 0) return false; if(n == 1) return true;//4的零次方 //用无符号类型处理溢出情况 unsigned int ans = 1; //常规的枚举,注意4的15次方大概就超了 for(int i = 1; i <= 15;i++) { ans *= 4; if(ans == n) return true; } return false; } };
第五题:1492. n 的第 k 个因子
题目描述
1492. n 的第 k 个因子 给你两个正整数 n 和 k 。 如果正整数 i 满足 n % i == 0 ,那么我们就说正整数 i 是整数 n 的因子。 考虑整数 n 的所有因子,将它们 升序排列 。请你返回第 k 个因子。如果 n 的因子数少于 k ,请你返回 -1 。 示例 1: 输入:n = 12, k = 3 输出:3 解释:因子列表包括 [1, 2, 3, 4, 6, 12],第 3 个因子是 3 。 示例 2: 输入:n = 7, k = 2 输出:7 解释:因子列表包括 [1, 7] ,第 2 个因子是 7 。 示例 3: 输入:n = 4, k = 4 输出:-1 解释:因子列表包括 [1, 2, 4] ,只有 3 个因子,所以我们应该返回 -1 。 示例 4: 输入:n = 1, k = 1 输出:1 解释:因子列表包括 [1] ,第 1 个因子为 1 。 示例 5: 输入:n = 1000, k = 3 输出:4 解释:因子列表包括 [1, 2, 4, 5, 8, 10, 20, 25, 40, 50, 100, 125, 200, 250, 500, 1000] 。 提示: 1 <= k <= n <= 1000
解题报告
常规枚举,我没有get到这个题的考点,可恶,菜到都不知道人家的题目考什么了
参考代码(C++版本)
class Solution { public: int kthFactor(int n, int k) { //升序排列倒是不必太在意,从小到大枚举就好 //直接枚举吧 int cnt = 0;//计数器 for(int i = 1; i <= n;i++) { if(n % i == 0) { cnt++; if(cnt == k) return i; } } return -1; } };
第六题:279. 完全平方数
题目描述
279. 完全平方数 给你一个整数 n ,返回 和为 n 的完全平方数的最少数量 。 完全平方数 是一个整数,其值等于另一个整数的平方;换句话说,其值等于一个整数自乘的积。例如,1、4、9 和 16 都是完全平方数,而 3 和 11 不是。 示例 1: 输入:n = 12 输出:3 解释:12 = 4 + 4 + 4 示例 2: 输入:n = 13 输出:2 解释:13 = 4 + 9 提示: 1 <= n <= 104
解题报告
这个题是一个完全背包。
完全平方数就是物品(可以无限件使用),凑个正整数n就是背包,问凑满这个背包最少有多少物品。
那就直接拿出我可爱的闫式DP分析法吧。
完全背包的背景是如下分析的:
对于这个题而言,只是需要重新定义一下集合 :f[i]表示和为i的完全平方数的最少数量
参考代码(C++版本)
class Solution { public: int numSquares(int n) { int f[n+1]; //让结果初始化为正无穷 memset(f,0x3f,sizeof f); //初始化 f[0] = 0; //开始DP for(int i = 1; i <= n;i++) //因为第一维的i是直接可以去的,所以上的优化为一维的完全背包递推公式 for(int j = 1; j *j <= i;j++) f[i] = min(f[i-j*j]+1,f[i]); //输出结果 return f[n]; } };
三、今日收获
一、对整数溢出的处理
之前在其他平台做题,也可能是自己做得少,但是通过这两天的Lc写题以后,感觉它考察了很多关于溢出的问题。
二、递归和循环的灵活转换